1 Introduction

This part of the core Physics unit concerns the development of the the theory and application of Electric and Magnetic fields and their unification into the theory of Electromagnetism. At school, before you came to univeristy, you have been introduced to all the basic concepts and ideas about electrostatic and magnetostatic fields and electromagnetism. You will have been introduced to the ideas of,

electric charge, Coulomb’s law and the concept of electric fields around charges,
magnetism and the fields arising from flowing currents,
electric and magnetic fields in materials (for example dielectrics),
and that light is an electromagnetic wave.

How do I know this?

Well here are some typical questions from GCSE and GCE (A level) exam papers. If you did not do these qualifications you should have covered them in similar qualifications. These snippets are taken from the AQA exam board.

AQA GCSE

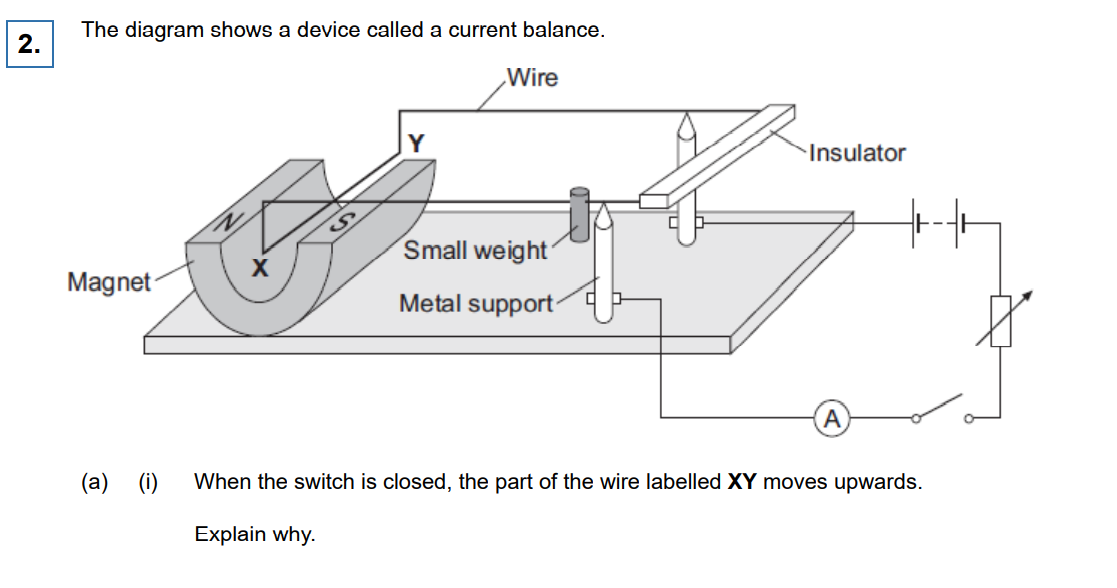
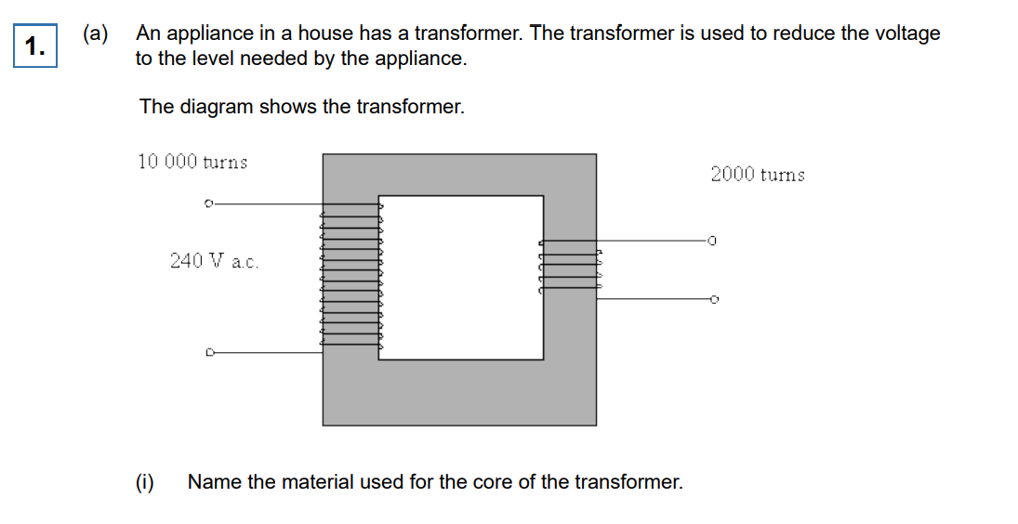
AQA GCE (A Level)

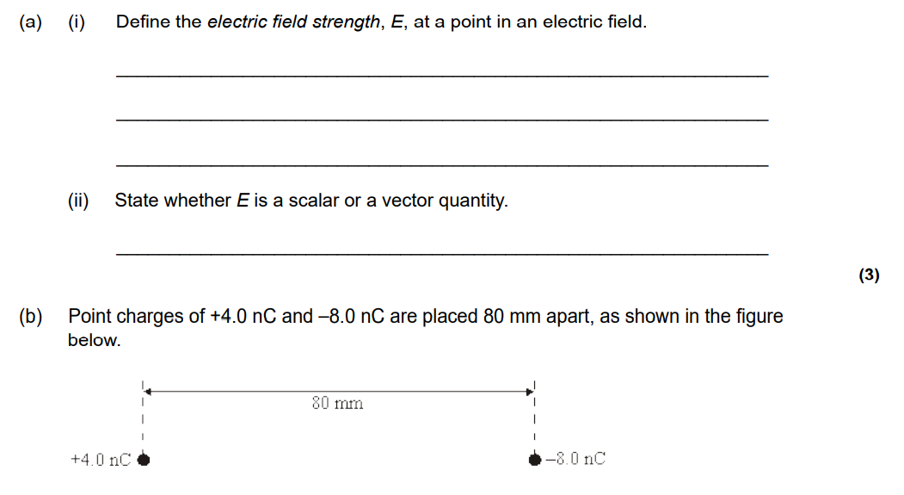
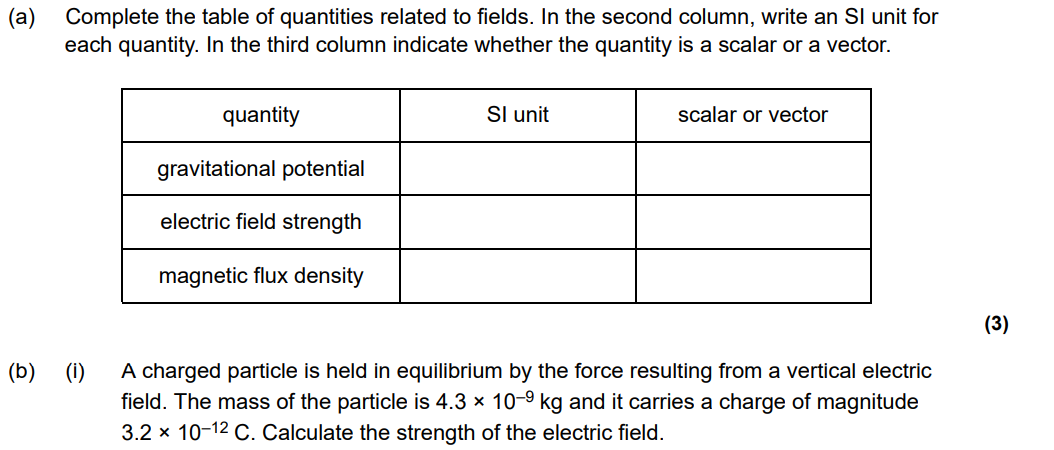
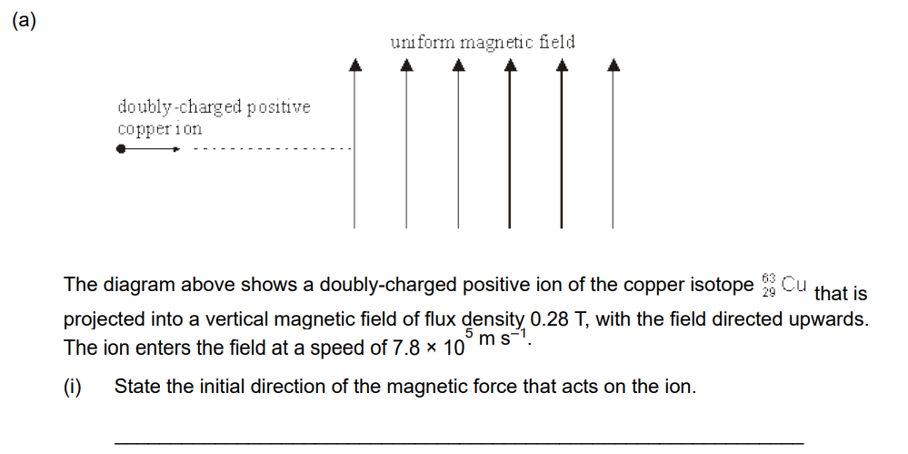
You’ve probably also come across ideas such as Fleming’s left-hand (for motors) and right-hand rule (for generators) and equations such as

$F=Bil\sin(\theta)$

So what else is there to learn?

Well hopefully you now know a lot more about vectors and especially vector calculus. So in this course we are going to revisit these ideas to make use of this new mathematical knowledge to obtain a deeper understanding of the physics and mathematics that underpins the classical theory of electromagnetism. To emphasise this point I’m now going to give you the theory of electromagnetism as encapsulated in Maxwell’s equations,

$\nabla.\vec{E}=\rho/\epsilon_0$, $\nabla.\vec{B}=0$, $\nabla\times\vec{E}=-(\partial\vec{B}/\partial t$), $\nabla\times\vec{B}=\mu_0\vec{J}+\mu_0\epsilon_0(\partial\vec{E}/\partial t$).

It is these, in addition to the force law,

$\vec{F}=q(\vec{E}+\vec{v}\times\vec{B})$,

that are the equations that are needed to cover Classical Electromagnetism, although it is important to note that Maxwell’s equations by themselves are relativistically correct.

You will also have discussed electric fields in terms of the electric potentials or potential differences (for example the potential difference between the terminals on a battery) but you may have wondered whether there was such a thing as a magnetic potential. It turns out the answer is yes, but, as they say it is complicated, as we can’t express the magnetic potential in terms of a scalar field, but rather we need to introduce the idea of a vector potential. In doing this we can write Maxwell’s equations in terms of the electric potential ,$V$ and magnetic (vector) potential $\vec{A}$ as,

$\nabla^2 V-\mu_0\epsilon_0(\partial ^2 V/\partial t^2)=-(1/\epsilon_0)\rho$,

and

$\nabla ^2 \vec{A}-\mu_0\epsilon_0(\partial ^2 \vec{A}/\partial ^2 t)= -\mu_0 \vec{J}$.

In this course we will not discuss the magnetic vector potential in any great detail, but it is introduced as it, along with the electric potential, underpins much of the treatment of electromagnetism in advanced courses on quantum mechanics and relativistic physics.

You might also note, but we won’t use it here, that $V$ and $\vec{A}$ together form a four-vector - something you’ve seen in your relativity course.

1.1 Electromagnetism and vectors

Hopefully, from the introduction, you are now convinced that a thorough grounding in vectors and vector calculus is an important pre-requisite for this course. You will only have seen some of this mathematics in the last few weeks, indeed, some of the material you will only just be covering in your mathematics course now. At first you might find this quite difficult, but hopefully, as you work through the examples and ideas in this course, you will come to appreciate the power and utility of the vector approach.

Before we move on you should note that there are many different ways that you may write vectors. In print, you will often see them written as above with an arrow above the symbol (e.g. $\vec{E}$), but you will find other texts (Griffuiths for example) where bold fonts (e.g. $\bf{E}$) or underlined characters (e.g. $\underline{E}$) are also used. You should be aware of this and be prepared to interpret any of them as valid ways to portray a vector. However, when $\textit{you are doing}$ maths you need to take especial care to distiguish scalars, vectors and components of vectors when writing your solutions. Again, there are many ways in which this may be done and different people will use slightly different notation. However, it is very important that when you are writing your solutions to problems, and in exams, that you make clear distinctions between scalars, vectors, components of vectors etc. It is for this reason that I will not produce lecture slides with text formatted equations - I want you to see hand-written presentations of the mathematics. However, as in the case for printed vector formalisms there are many ways that scalar and vector quantities may be written, e.g.

In my lectures I will use the following notation,

but I am happy to accept any commonly used notations in your solutions to problems, provided you are clear and consistent. You may find I sometimes slip into using $\textbf{i,j,k}$ (or equivalent i, j, k formats) in lectures as they are a very common way of writing unit vectors in maths courses. However, $ i, j$ and $\textbf{i,j}$ are commonly used symbols for current and current density in electromagnetic notation which can lead to confusion! You can usually distinguish the use by the context in which they are used.

1.2 Resources

As explained, I will not produce pre-prepared lecture slides - the lecture material will be presented in ‘real time’. These notes, that accompany the lectures, are not meant to be a comprehensive resource. They cover the key points and ideas required for our discussion of electromagnetism, but they are not meant to be the only resource you should use. The text for this course is “Introduction to Electrodynamics” by Griffiths (Cambridge University Press). There are copies of the book in the library and you have access to the electronic through the Univeristy. You should already have used chapter 1 as the basis of your mathematics course on vector analysis. The relevant parts of this book for this course are chapters 2 to 7. I will make reference to Griffiths continually through the lectures. However, there are some sections of the chapters that we will not cover. I will mention these as we proceed and you will not need to learn the material in them. However, I would still strongly recommend you read them for the full context of the electromagnetim course.

With this said, lets start!

Return to Index