13 Fields in Matter
13.1 Introduction
So far in our discussion of electromagnetism we have largely confined our discussion of the electric and magnetic fields to points in space away from their sources. That is at distances away from charge distributions and current carrying wires. At a few points in our examples we have also asked what happens to the field inside regions of uniform charge density or current densities (the electric field in a sphere of charge or the magnetic field in a current carrying wire). But what happens to the electric and magnetic fields when they interact with real materials? This is a difficult problem that needs a good understanding of quantum mechanics to address properly (for example, we cannot understand semiconductors without it). So how was this addressed in the 19th century (before the theory of quantum mechanics was developed)? Well a more phenomenological approach was used. This is the approach we are going to use here. A thorough and rigurous description of the theory is presented in Griffiths chapters 4 and 6. I strongly recommend you read those sections in addition to these notes. However, the main aim in this course is to introduce you to the concepts of the auxiliary fields (\(\vec{D}\), the Displacement field) and the (\(\vec{H}\)) field. In particular we consider the case of linear materials; these include dielectrics, diamagnets and paramagnets. In passing we will mention non-linear materials and those that generate permanent electric and magnetic fields (ferroelectrics and ferromagnets) but they will not be considered in any detail.
13.2 Maxwell’s equations in matter
At the end point of our discussion we want to reach the equivalent for Maxwell’s equations in matter. I state them here,
\(\displaystyle \nabla\cdot\vec{D}=\rho_f\)
\(\displaystyle \nabla \times \vec{E} = -\frac{\partial \vec{B}}{\partial t}\)
\(\displaystyle \nabla\cdot\vec{B}=0\)
\(\displaystyle \nabla\times\vec{H}=\vec{J_f}+\frac{\partial \vec{D}}{\partial t}\).
We can already note that two of these equations are unchanged from what we’ve already seen, but for the other two equations we have introduced two new ‘sources’, \(\rho_f\) and \(\vec{J_f}\) and two new fields, \(\vec{D}\) and \(\vec{H}\). The new fields are related to the electric and magnetic fields by,
\(\vec{D}=\epsilon_0\vec{E}+\vec{P}\)
\(\vec{H} = \frac{1}{\mu_0}\vec{B}-\vec{M}\)
so our task is to understand what the vectors \(\vec{P}\), the polarization and \(\vec{M}\) the magnetization mean when we are discussing the properties of materials. In order to conceptualize the behaviour of the fields we’ll also need to establish what we mean by \(\rho_f\), the ‘free’ charge and \(\vec{J_f}\) the ‘free’ currents.
We should note at this point that polarization and magnetization can occur in the absence of external electric or magnetic fields (your typical bar magnet produces a magnetic field without needing any external wires) but in this course we will only consider ‘linear’ materials. These are materials in which, in the absence of any external electric fields or magnetic fields, there is no electric or magnetic field present, but they become polarised/magnetized in the presence of an external field in a way in which the polarization/magnetization is proportional to the external field. This ‘linear response’ is encapsulated in the expressions,
\(\displaystyle \vec{P}=\epsilon_0\chi_e\vec{E}\)
\(\displaystyle \vec{M}=\chi_m\vec{H}\).
we note that \(\chi\) occurs as a common symbol in physics and is often associated with the concept of ‘susceptibility’ and so here \(\chi_e\) and \(\chi_m\) are known as the electric and magnetic suscpetibility respectively. The more susceptible the material is to the electric or magnetic field the larger the polarisation or magnetization will be. Not all materials need to respond in this linear way but we will confine our discussion, in this course to linear materials, only. Note the use of \(\vec{H}\) when defining \(\vec{M}\). This When we do this it enables us to reduce our description of the relation between \(\vec{D}\) and \(\vec{E}\), and \(\vec{H}\) and \(\vec{B}\) to simple constants such that,
\(\displaystyle \vec{D}=\epsilon_r \epsilon_0 \vec{E}\)
and
\(\displaystyle \vec{H}=\frac{1}{\mu_r \mu_0}\vec{B}\)
where \(\epsilon_r\) is known as the relative permitivity (sometimes known as the dielectric constant) and \(\mu_r\) the relative permeability of the material. You may have come across these previously but it is important to note that they assume this linear response.
Now one might think, by substituting \(\vec{D}=\epsilon_r \epsilon_0 \vec{E}\) and \(\vec{H}=\frac{1}{\mu_r}{\mu_0}\vec{B}\) into our new equations that we introduced at the beginning of this section, that we recover our original Maxwell equations apart from factors of \(\epsilon_r\) and \(\mu_r\) and you are correct. Indeed, in all we did before, subsitituing \(\epsilon = \epsilon_r\epsilon_0\) in place of \(\epsilon_0\) and \(\mu=\mu_r\mu_0\) in place of \(\mu_0\) will give all the results and equations we found before. This is fine and works \(\textit provided\) we stay within the material. However, the minute we cross boundaries with different materials (and the vacuum) we have to take care as our standard relationships between charge and field and current and field can become false friends! For example, for static fields we don’t always have \(\nabla \times \vec{D}=0\) away from charges and so we are not always able to introduce a simple scalar potential for solving our problems. This is discussed fully in Griffiths, but in the special cases and examples you will see here (especially those with high symmetry) we can recover and use familiar ideas (such as Gauss’ law) to solve problems.
Students often ask why we introduce \(\vec{D}\) and \(\vec{H}\) - it seems to add complexity to problems if all we need to do is to convert to \(\vec{E}\) and \(\vec{B}\) and use \(\epsilon_r\) and \(\mu_r\). However, it is when we consider what happens to the fields at the boundaries between materials that their utility becomes apparent. Hence, an important part of this course is to understand the boundary conditions for \(\vec{D}, \vec{H}, \vec{E}\) and \(\vec{B}\) and how they are used to solve problems. In the waves section of the course you will see how these boundary conditions give rise to for example the refractive index of glasses etc.
In the next sections we will discuss what we mean by polarization and magnetization.
13.3 Induced dipoles and polarization.
If you have a basic knowledge of chemistry you will know that many molecules (for example water, hydrogen chloride (HCl) etc.) have a small separation of the charge on them ( for example, in a simple picture, in water the oxygen atoms have a small negative charge and the hydrogen a small positive charge, in HCl the chlorine is slightly negative and the hydrogen slightly positive). Hence, the molecules have a permament dipole moment (\(\vec{p}\)). It is possible, in some materials (ferroelectrics), that these may sponataneously line up such that a crystal may end up with a permanent electric field around it. We will not consider materials such as these here. More generally (as in water) these dipoles will be randomly oriented so that the net field is zero for the bulk material. However, if we apply an external electric field we can see that the molecular dipoles will begin to line up so that the bulk material itself will start to have a polarization \(\vec{P}\) itself. Indeed our formal \(\textit definition\) of polarization is that,
\(\vec{P}\) is the dipole moment per unit volume of a material.
The alignment of polar molecules in an external electric field is not the only mechanism by which materials may be polarized. For example, atoms themselves will become polarized in an electric field (the nucleus moves slightly with respect to the centre of the electron cloud, see Griffiths for details). Similarly, in ionic materials, the positive and negative ions will tend to move in response to external field. In other words we imagine the polarization \(\vec{P}\) to be the result of the ‘lining’ up of the many tiny dipoles aligned or created by the external field. in a simple way we can imagine the dipoles line up as in this figure,
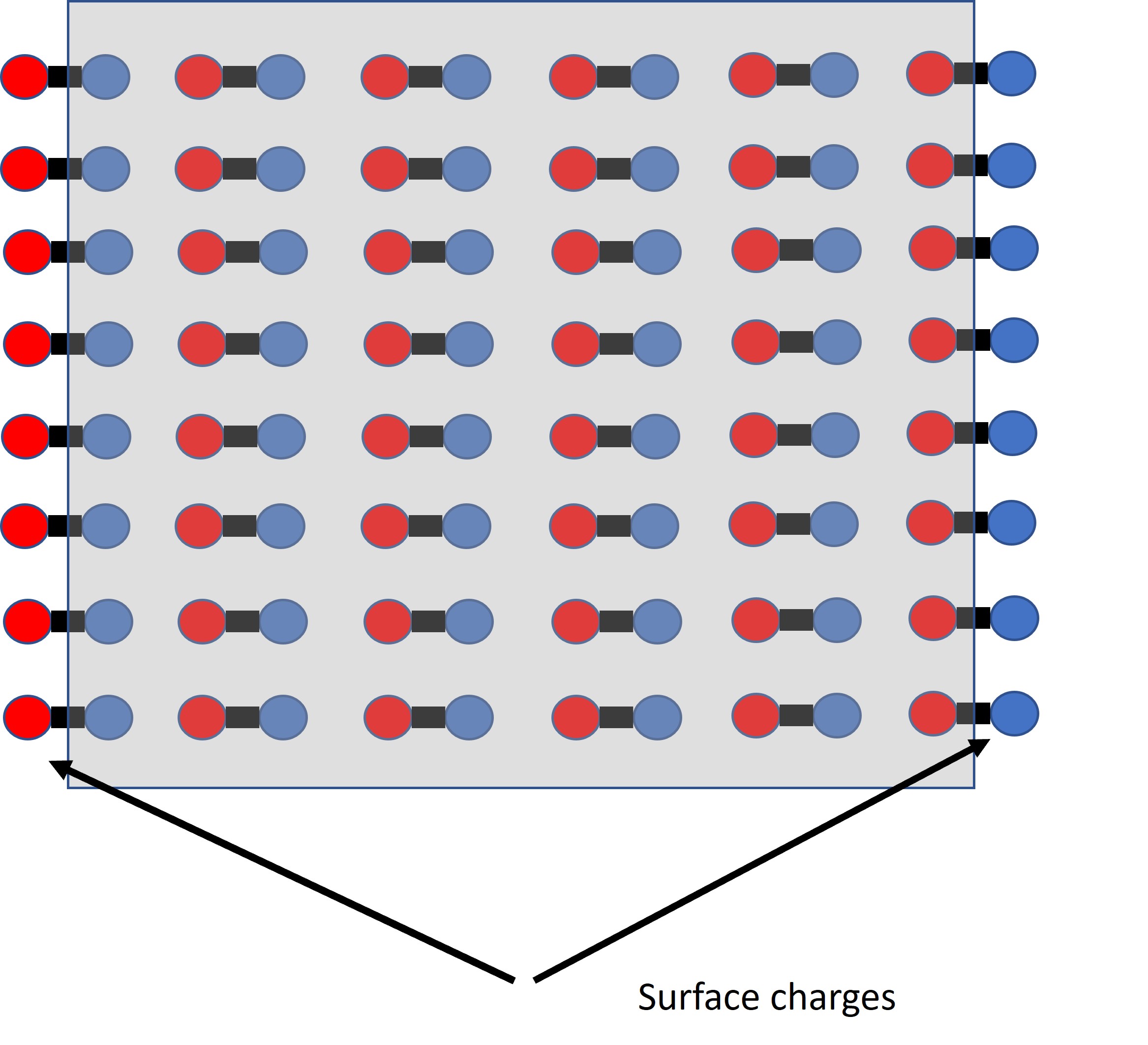
Here the negative and positive parts of the induced/aligned dipoles are shown as blue and red. (Note, in real materials aligned permanent dipoles would still show some randomness in their orientation in the external field. If the field becomes too strong, the dipoles will end up almost perfectly aligned, the polarization becomes ‘saturated’ and we no longer have a linear material).
From the figure we see that in the shaded grey box the net charge is zero on the macroscopic scale (i.e. at the point where we can’t ‘see’ individual dipoles). However, at the edges of the grey box we see that there is a net positive charge on one side and a next neagtive charge on the opposite side. These are known as the surface charges on the dielectric so that, more generally for any surface on our dielectric, we can describe a ‘bound’ surface charge density \(\sigma_b\). These are known as bound charges as they must remain on the surface (they can’t detach from the bit of the dipole in the grey box) and can’t move around. Also, the net surface charge on the surface of the dielectric must be zero. For a linear material, if the external field is removed the surface charges ‘melt’ back into the bulk.
What can we learn about these bond charges?
Well, we know the electrostatic field from a dipole, we saw it in our discussion of electrostatics,
\(\displaystyle V_{dipole}(\vec{r})=\frac{1}{4\pi\epsilon_0}\frac{\vec{p}\cdot \hat{\vec{r}}}{r^2}\)
Now let’s write the dipole moment for one of these small dipoles (which we will assume has a volume \(d\tau'\)) as (remember we defined the \(\vec{P}\) as the dipole moment per unit volume),
\(\displaystyle \vec{p}=\vec{P}d\tau'\).
There are a few steps here in thinking how we go from the idea of individual dipoles to the definition of the bulk polarization, but we think of \(d\tau'\) as being large enough not to see the discrete nature of the individual dipoles. from this definition of \(\vec{p}\) (remembering these are induced dipoles) we can use the principle of superposition to find the potential over and around the whole material, i.e.
\(\displaystyle V(r)=\frac{1}{4\pi\epsilon_0}\int_{Vol\;\;dielectric}\frac{\vec{P}(\vec{r'})\cdot\hat{\vec{r}}}{r^2}d\tau'\).
We can rewrite this by noting,
\(\displaystyle \nabla'\left(\frac{1}{r}\right) = \frac{\hat{\vec{r}}}{r^2}\)
so that ,
\(\displaystyle V(\vec{r})=\frac{1}{4\pi\epsilon_0}\int_{Vol}\vec{P}.\nabla'\left(\frac{1}{r}\right) d\tau'\).
This can be integrated by parts to give,
\(\displaystyle V(\vec{r})=\frac{1}{4\pi\epsilon_0}\left[\int_{Vol}\nabla'\cdot\left(\frac{\vec{P}}{r}\right)d\tau'-\int_{Vol}\frac{1}{r}(\nabla'\cdot\vec{P})d\tau'\right]\)
If we apply the divergence theorem to the left-hand integral we get,
\(\displaystyle V(\vec{r})=\frac{1}{4\pi\epsilon_0}\oint_S\frac{1}{r}\vec{P}\cdot d\vec{a'}-\frac{1}{4\pi\epsilon_0}\int_{Vol}\frac{1}{r}(\nabla'\cdot\vec{P})d\tau'\)
that we write finally as,
\(\displaystyle V(\vec{r})=\frac{1}{4\pi\epsilon_0}\oint_S\frac{\sigma_b}{r}da'+\frac{1}{4\pi\epsilon_0}\int_{Vol}\frac{\rho_b}{r}d\tau'\)
where we have introduced \(\sigma_b\equiv \vec{P}\cdot\hat{\vec{n}}\) and \(\rho_b \equiv -\nabla\cdot\vec{P}\)
You don’t need to learn this derivation but the important point here is that we see the mathematical origin of the surface charge distribution we described above, it is just the dot product of the polarization at the surface and the normal vector to the surface. We also see that we have a second term \(\rho_b\), the bound bulk charge density. What is this and why didn’t we see it earlier in our description? Well, firstly if \(\vec{P}\) is uniform in the material (as in our diagram) then \(\nabla\cdot\vec{P}=0\) so \(\rho_b=0\). If however, \(\vec{P}\) varies in the material (i.e. some regions of higher polarization within), then we see some internal bound charge distribution. Like the surface charges this would disappear for linear materials if the external field is removed and the bound charges can’t freely move within the material.
What do we understand from this? Well, if we know the polarization of the material (it could even be permanently polarised or a non-linear material at this point) we can always find the surface and bulk bound charge densities. Make sure you understand the concept of these ‘bound’ charges.
13.4 The displacement field \(\vec{D}\).
We can use the result above to learn more about the electric fields in our materials. The bound charge densities are ‘real’ and will produce electric fields as we’ve seen before. In our system (especially if we are applying external electric fields) we will also expect to see some ‘free’ charges (for example, charges building up on metals plates that are generating the external field). Hence to work out the electric field we need to calculate the effects of the bound charges (\(\rho_b\)) and any other charge distributions \(\rho_f\) present, i.e.
\(\displaystyle \rho = \rho_b+\rho_f\).
We can now apply Gauss’ law (Maxwell’s equation number 1) to all these charges to get,
\(\displaystyle \epsilon_0\nabla\cdot\vec{E}=\rho=\rho_b+\rho_f=-\nabla\cdot\vec{P}+\rho_f\).
We can rearrange this so that
\(\displaystyle \nabla\cdot(\epsilon_0\vec{E}+\vec{P})=\rho_f=\nabla\cdot\vec{D}\)
where we have defined
###From this we get our result,
###which,as we saw for \(\vec{E}\) gives the result,
\(\displaystyle \oint\vec{D}\cdot d\vec{a}=Q_{free}\).
Again these relations are true for non-linear materials (all we need to know is \(\vec{P}\)) but there is a false familiarity you might get from 13.2. The problem is (think permanently polarized materials) that we don’t necessarily have \(\nabla \times \vec{D}=0\). Hence, our use of electric potentials for \(\vec{D}\) has to be used with care. If you check and have \(\nabla\times\vec{D}=0\) then you are OK. For details see Griffiths 4.3.2.
You may note that we haven’t mentioned \(\sigma_b\) above. What happened to it? Well we used a slight of hand. We don’t really need to use \(\sigma_b\) at all, we can wrap it all up in the \(function\) \(\rho_b\) close to surface. So, it all depends how we consider the vector \(\vec{P}\) at the boundary. Is the change in \(\vec{P}\) at the surface abrupt (mathematically discontinuous) or does it go to zero with a continuous change? If the former, what is the polarization at the surface? If the latter we can think of the surface charge density as the thin layer (thickness) over which \(\vec{P}\) goes to zero from its bulk value.
13.5 The boundary conditions for \(\vec{D}\).
As we mentioned previously, the definition of \(\vec{D}\) is partciularly useful when we consider the boundaries between materials. Without derivation, I’ll quote the boundary conditions for \(\vec{D}\) here. If you want to see how to arrive at the them see Griffiths. (Again note that these apply in the most general case (linear and non-linear materials).
###13.6 Linear dielectrics.
In the defintion of \(\vec{D}\) we did not say how the material became polarized. IN the case of linear dielectric we relate the polaraization explicitly to the strength of the external field and we assume the relatioship is linear. We define the constant of proportionality as \(\chi_e\) and we write,
\(\displaystyle \vec{P}=\epsilon_0\chi_e\vec{E}\)
Note we have have used \(\epsilon_0\vec{E}\) to represent the external field (we could have wrapped \(\epsilon_0\) up in the definition of \(\chi_e\)).
Once we’ve established this relationship between \(\vec{E}\) and \(\vec{P}\) we can eliminate \(\vec{P}\) in our definition to give,
\(\displaystyle \vec{D}=\epsilon_0\vec{E}+\vec{P}=\epsilon_0\vec{E}+\epsilon_0\chi_e\vec{E}=\epsilon_0 (1+\chi_e)\vec{E}\).
Hence for the case of linear dielectrics we can express \(\vec{D}\) as
###where \(\epsilon\) is the permitivity of the material. This may be expressed alternatively as,
\(\displaystyle \epsilon=\epsilon_r\epsilon_0=\epsilon_0(1+\chi_e)\)
where \((1+\chi_e)=\epsilon_r\) is known as the relative (to free space) permittivity (or sometimes as the dielectric constant).
13.7 Why use \(\vec{D}\)?
So the question might be why do I use \(\vec{D}\)? Well, if we wanted to do our cacluations with \(\vec{E}\) we would need to know the bound surface and bulk charge densities plus any free charges in order to work out the electric field. By using \(\vec{D}\) we only need to consider the free charges (for example the charges on the plate of a charged capacitor that produces a field across our dielectric - there is a problem about this where you can show \(C=\epsilon_r C_{vac}\) for a capacitor with a dielectric between its plates) and the polarization. We can translate our results for \(\nabla\cdot\vec{E}=\frac{\rho}{\epsilon_0}\) to \(\nabla\cdot\vec{D}=\rho_f\) and \(\oint\vec{D}\cdot d\vec{a}=Q_{free}\). However, we must be careful, as we pointed out earlier, as \(\nabla\times \vec{D}\) may not be zero at which point anything we deduced from \(\vec{E}\) being a conservative field is no longer true. (In words this means in general there is no Coulomb’s law that can be applied to the free charges - we have to take account of all charges in the system using \(\vec{E}\)). Why is this so, well look at \(\nabla \times \vec{D}\).
\(\displaystyle \nabla \times \vec{D}=\epsilon_0(\nabla\times \vec{E})+\nabla\times\vec{P}\).
We know \(\nabla\times \vec{E}\) is always zero. However, it is not always true that \(\nabla\times\vec{P}\) is zero (i.e. ferroelectrics, electrets …). Hence, provided we can say \(\nabla\times\vec{P}=0\) (often in the case of high symmetry, or if you know the function for \(\vec{P}\)) we can revert back to our knowledge of \(\vec{E}\) to help us solve problems.
The best way to understand the use of \(\vec{D}\) is to go through the examples and problems. In most cases rthe symmetry of the problems allows us to make simple assumptions about \(\vec{D}\) and \(\nabla\times\vec{D}\).